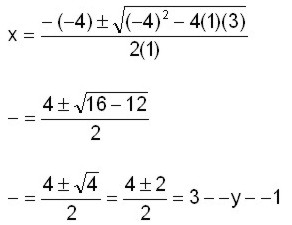Unidad V: Ecuaciones algebraicas.
Cualquier expresión que incluya la relación de igualdad (=) se llama ecuación.
Una ecuación se denomina identidad si la igualdad se cumple para cualquier valor de las variables; si la ecuación se cumple para ciertos valores de las variables pero no para otros, la ecuación es condicional.
Resolución de ecuaciones cuadráticas
Dada una ecuación de segundo grado o cuadrática en su forma general:
ax2 + bx + c = 0
hay diversas posibilidades para resolverla dependiendo de la naturaleza específica de la ecuación en cuestión.
Si la ecuación se puede factorizar, la solución es inmediata. Por ejemplo: x2 – 3x = 10
Primero se escribe la ecuación en su forma general: x2– 3x –10 = 0
que se puede factorizar como: (x – 5) (x + 2) = 0
La igualdad sólo se cumple cuando uno de los factores (x – 5 y x + 2 son los factores) es cero. Para que ello ocurra, x debe ser = 5(5 – 5 = 0) o x debe ser = –2 (–2 + 2 = 0) . En ese caso, uno cualquiera de los factores multiplicado por cero es igual a cero.
Éstas son las soluciones de la ecuación, que de nuevo se pueden verificar mediante sustitución.
Si a primera vista no se encuentra un modo directo de factorizar la ecuación, puede existir otra alternativa.
Por ejemplo, en la ecuación 4x2 + 12x = 7
la expresión 4x2 + 12x se podría factorizar como un cuadrado perfecto si fuera 4x2 + 12x + 9, que equivale a (2x + 3)2.
Esto se puede conseguir fácilmente sumando 9 al lado izquierdo de la ecuación.
La misma cantidad debe sumarse, por supuesto, al lado derecho:
4x2 + 12x + 9 = 7 + 9
(2x + 3)2 = 16
que se reduce a ![]()
o 2x + 3 = +4 y 2x + 3 = –4
pues ![]() tiene dos valores.
tiene dos valores.
La primera ecuación da la solución x = 1/2 (restando 3 de ambos lados: 2x = 1, y dividiendo ambos lados por 2: x = 1/2).
La segunda ecuación da x = –7/2.
Ambas soluciones se pueden verificar como antes, sustituyendo los valores en cuestión en la ecuación original.
Esta forma de resolución se suele denominar método del cuadrado perfecto.
En general, cualquier ecuación cuadrática de la forma
ax2 + bx + c = 0
se puede resolver utilizando la fórmula cuadrática.
Para cualquier ecuación de este tipo las dos soluciones de x están dadas por la fórmula:
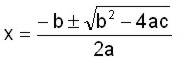
Por ejemplo, para encontrar las raíces de
x2 – 4x = –3
primero se pone la ecuación en su forma general:
x2 – 4x + 3 = 0
Para entender lo que sigue, recordemos que x2 es igual a 1x2, y para aplicar la fórmula cuadrática anterior debemos reconocer
a, b y c dentro de esta forma general.
Para ello, hacemos a = 1, b = –4 y c = 3.
Estos valores se sustituyen en la fórmula cuadrática: